|
Районная
олимпиада по математике 2004-2005 учебный год
11 класс
1. В
кубе АВСDА1В1С1D1
построить сечение, проходящее через три точки, лежащих на серединах
рёбер АВ, ВС и СС1 и найти его площадь.
(4 балла)
2. Сократима
ли дробь 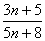 при
каком-нибудь значении n?
(4 балла)
3.
Решить
уравнение (х2-х-1)2 = х3+5.
(4 балла)
4.
Найти наибольшее
значение выражения 3х+у при условии у
 - .
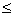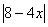(4 балла)
5. Можно
ли квадрат размером 10х10 клеток составить из фигурок, каждая из которых
представляет собой 4 клетки, расположенные в форме буквы Т
(4 балла)
6. Найти
f(х),
если при всех х выполнено равенство 2 f(х-1)+3
f(1-х) = х2.
(4 балла)
7. Замкнутая линия на
плоскости такова, что у любого вписанного в неё четырёхугольника сумма
противоположных углов равна 180○.
Докажите, что эта линия – окружность.
(4 балла)
Посмотреть задания 10 класса |
