|
Районная
олимпиада по математике 2004-2005 учебный год
10 класс
1.
Решить
уравнение (х2+4х)2 + (х+2)2 – 10 = 0.
(4 балла)
2. Найти
наименьшее значение выражения
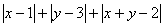
(4 балла)
3. Для
каждого значения параметра определить число решений уравнения
(4 балла)
4. Точка
Р лежит внутри правильного треугольника АВС со стороной 1. Точки К,
L и
M – основания перпендикуляров, опущенных из точки Р
на стороны ВС, АС и АВ соответственно. Найти
BK+ CL+ AM.
(4 балла)
5. На
сторонах ВС и СD квадрата АВСD
со стороной 1 взяты точки
M
и
N
так, что угол
MAN
равен 45 .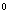
Найти периметр треугольника
CMN.
(4 балла)
6.
Может
ли 5n-1 делиться на 4n-1 при каком-нибудь
натуральном
n?
(4 балла)
7.
Дано
n
чисел, каждое из которых равно 1 или -1. . Известно, что х1х2
+х2х3 + …+хnх1=0.
Докажите, что
n
делится на 4
Посмотреть задания 9 класса
Посмотреть задания 11 класса |
