|
Районная
олимпиада по математике 2005-2006 учебный год
10 класс
1.В
каждой из двух урн находится произвольное не равное нулю число шаров.
Разрешается одновременно удалять из урн одинаковое число шаров и
удваивать число шаров в одной из урн. Доказать, что с помощью этих
операций можно удалить из урн все шары.
(4 балла)
2. Найти
наименьшее число, при делении которого на 2 получается точный квадрат, а
при делении на 3 –точный куб.
(4 балла)
3. Существует
ли многогранник, имеющий ровно 7 ребер?
(4 балла)
4.Пять
отрезков таковы, что из любых трех можно составить треугольник.
Доказать, что хотя бы один из этих треугольников остроугольный.
(4 балла)
5.Доказать,
что при всех значениях а и
b
справедливо неравенство:
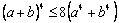
(4 балла)
6.В
турнире по футболу участвовало
n
команд. Известно, что ни один из матчей не закончился вничью. Доказать,
что сумма квадратов чисел, задающих количество побед каждой команды
равна сумме квадратов чисел, задающих количество их поражений.
(4 балла)
7. Дан
прямоугольный треугольник АВС с катетами АВ =8 и ВС = 6. Проведена
медиана ВМ. Прямая
l
параллельна АВ и пересекает отрезки АМ, ВМ и ВС соответственно в точках
P,
Q,
R.
Найти наименьшее значение SPMQ+SBQR.
(4 балла)
Посмотреть задания 9 класса
Посмотреть задания 11 класса |

