|
Районная
олимпиада по математике 2005-2006 учебный год
10 класс
1. Вычислить
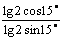 . .
(4 балла)
2. В
турнире по футболу участвовало
n команд.
Известно, что ни один из матчей не закончился вничью. Доказать, что
сумма квадратов чисел, задающих количество побед каждой команды равна
сумме квадратов чисел, задающих количество их поражений.
(4 балла)
3. В
каждой клетке доски размером
NxM стоит
шашка. Играют двое. За один ход игрок может взять любое количество
подряд стоящих шашек в любом горизонтальном или вертикальном ряду. Ходят
по очереди. Выигрывает тот, кто возьмет последнюю шашку. Считаем, что
игроки играют наилучшим образом. Какой игрок победит. Укажите, как он
должен играть.
(4 балла)
4. Две
окружности касаются друг друга внешним образом в точке
D.
Прямая касается одной из них в точке А и пересекает другую в точках В и
С. Докажите, что точка А равноудалена от прямых
BD и
CD.
(4 балла)
5. Решите
уравнение х3–у3 = ху+61, где х и
у – натуральные числа.
(4 балла)
6. Сравнить
числа 99! И 5099.
(4 балла)
7. Длины
двух скрещивающихся ребер тетраэдра равны а, двух других –
b,
еще двух – с. Найти объем тетраэдра.
(4 балла)
Посмотреть задания 10 класса |

